며칠 동안 글을 안 올렸습니다.
뭐 놀면서 지낸 것은 아니고요. 책 쓰는 것에 집중하고 있었습니다.
아직 진행 중입니다. 목표 출간일을 이번 주말인데 가능할지 모르겠습니다.
그래도 틈틈이 공부는 하고 있습니다.
오늘 볼 주제는 볼린저 밴드입니다.
투자 공부하시면서 한 번쯤은 들어봤을 만한 이름입니다. 많이들 사용하시나요?
예전에 저도 이걸로 재미를 보긴 했습니다만.....

볼린저밴드는 대부분의 차트 프로그램에 기본적으로 들어있습니다.
일봉기준으로 설명해 보자면
중심선은 20일 이평선
상한선 = 중심선 + (20일 주가 표준편차) *2
하한선 = 중심선 - (20일 주가 표준편차) *2
모든 지표가 그러하듯, 이평선과 표준편차의 숫자는 절대적인 것은 아닙니다.
차트의 시간 프레임과 개인 선호도에 따라 달라질 수 있는 부분입니다.
대략 사용법은 상한선에 캔들이 닿으면 하락 예상, 하한선에 닿으면 상승 예상.
아주 단순한 논리입니다. 물론 전부는 아니겠죠.
오늘도 분석해 가며 이해해 보겠습니다.
볼린저 밴드는 통계를 기반으로 하는 지표입니다.
수학도 어려운데 통계까지 나옵니다.
(볼린저밴드에서 나오는 표준편차의 의미를 이해하기 위해서는 꼭 선행되어야 하는 설명입니다.)
학창 시절에 시험을 보고 나면 항상 평균을 구했던 적이 있습니다.
평균 구하는 방법은 굳이 언급하진 않겠습니다. 여기서 그리 중요하지도 않고요.
평균에 따라오는 것이 있죠, 분산, 표준편차
분산에 대해 봅시다

분산은 각 값과 평균값의 차이를 제곱한 것들의 평균입니다.
우리는 측정값들이 평균에서 얼마나 떨어져 있는가를 확인하고 싶은 겁니다.
방향이 반대(수식으로 계산하면 마이너스)인 것들이 있으므로 제곱을 해주는 거죠.
그런데 이 결과 값은 실제 분포되어 있는 값들과는 차이가 납니다.
당연히 제곱을 했으니 분포된 값은 심하게 뻥튀기가 되어 있을 겁니다.
원래대로 돌려야죠, 루트를 취해줍니다.
그 값이 표준편차입니다.
표준편차 값은 실제 분포된 정도를 잘 반영하고 있습니다.
표준편차가 크면 측정값들 중에 평균에서 멀리 떨어진 것들이 많다는 얘기입니다.
반대로 작으면 평균 근처에 모여있다는 얘기죠.
통계는 굉장히 다양한 곳에서 사용합니다. 다루는 단위도 다르고 기준도 다릅니다.
학자들이 잘하는 게 뭔가요. 현상에서 규칙을 찾아서 법칙으로 만들죠.
통계도 마찬가지입니다.
통계학자들이 우리가 방금 사용한 평균 표준편차에 대해서도 간단한 표준을 만들어놨습니다.
각기 다른 분포값들을 다루기 쉽게 만들었습니다.
그래프를 다룰 때 기준은 항상 원점이죠.
네 평균값을 0으로 만들었습니다. 더 나아가 표준편차는 1로 만들었습니다.

우리는 이걸 표준화(Standardization)라고 부릅니다.
왜? 편하거든요.
수능에서 표준점수를 사용합니다. 과목별 원점수로 비교하면 난이도가 다르기 때문에 누군가는 피해를 볼 수 있습니다. 그래서 수능점수를 표준화해서 비교하기 위해 표준화를 거친 점수, 즉 표준점수로 성적을 판단합니다. 더 이상의 자세한 설명은 생략합니다.
어차피 우리는 과정보다는 결과만 사용하면 됩니다.
표준편차 1은 그리스 문자 σ 를 사용합니다. '시그마'라고 읽습니다.
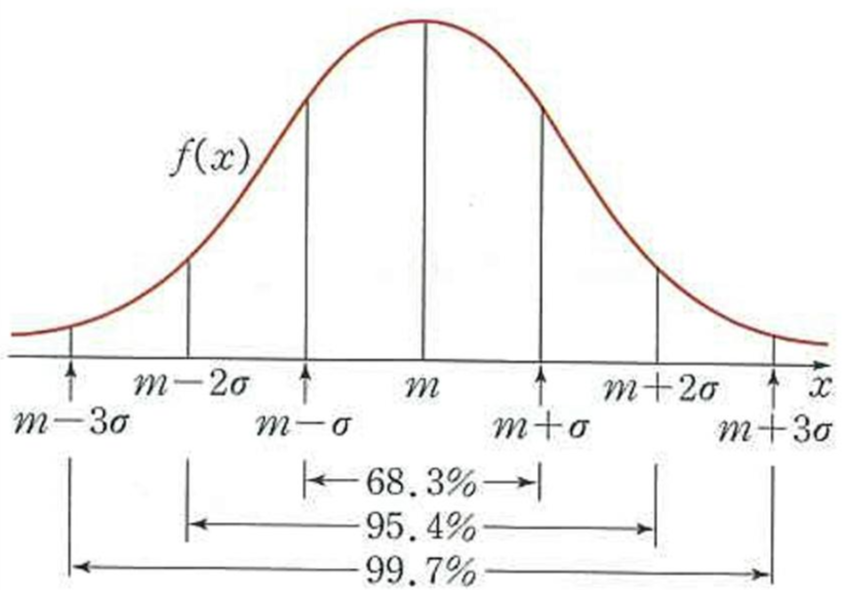
이 그래프에서 우리가 알아야 하는 것은 "2σ 안에 95%의 분포값이 존재한다"는 겁니다.
2σ를 벗어나는 것은 5% 이하의 확률입니다.
자 다 왔습니다.
다시 볼린저 밴드를 소환해 보겠습니다.
중심선은 20일 이평선
상한선 = 중심선 + (20일 주가 표준편차) *2
하한선 = 중심선 - (20일 주가 표준편차) *2
이걸 차트에 표현해 보면
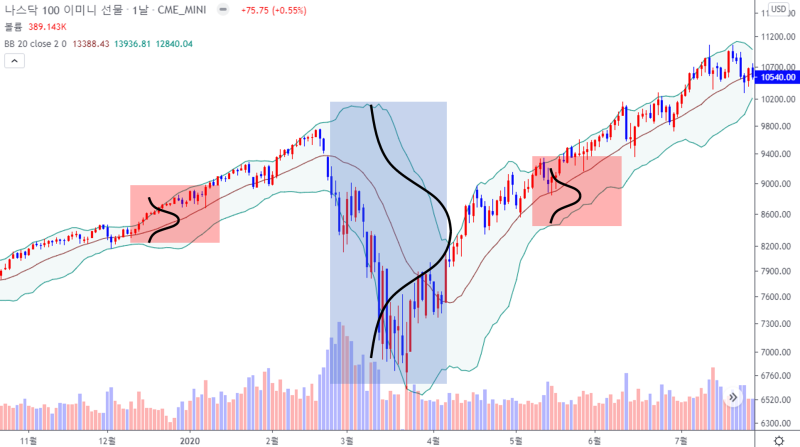
20일 이평선 기준으로 위아래 2σ에 해당하는 라인을 그려준 거죠.
다시 말해서 가격이 위아래로 움직이더라도 95%의 확률로 볼린저밴드 안에서 움직인다는 의미입니다.
대단하죠? 95%의 확률
그다지 어렵지도 않네요.
볼린저밴드를 공부하면 통계도 알아야 하고 뭔가 그럴듯하게 납득이 되는 설명과 함께 본인이 제법 똘똘해진 느낌을 받을 수 있습니다.
과연 투자에는 얼마나 도움이 될까요?
앞서 말한 볼린저 밴드 사용법
상한선 닿으면 하락 예상, 하한선 닿으면 상승 예상
어디서 많이 봤죠? 박스
상품가격이 박스권에서 오르락내리락할 때 유용하게 사용할 수 있습니다.
그런데, 추세나 튀는 값을 갖게 되면, 캔들이 상하한선에 붙어서 움직이는 경우가 있습니다.
꽤 많아요. 제가 봤습니다. ㅎㅎ 위에 차트에서도 보이죠.
뭔가 이것만으로는 불안합니다.
이를 보완하고자 밴드 내에서 값의 위치를 비율로 확인하는 %b, 밴드폭을 기준으로 변동성을 확인하는 스퀴즈 등의 보조 지표를 사용합니다.
%b는 밴드폭을 100으로 놓고 현재 값의 상하 위치를 %로 표시합니다.
밴드를 뚫고 상승, 하락하는 경우도 있으니 %b는 1을 넘거나 마이너스가 나오기도 합니다.
스퀴즈는 현재 값에서 밴드 폭을 측정해서 변동성 증가를 예측하는 방법입니다.

자세하게 알고 싶으신 분들은 '존 볼린저'옹 께서 직접 쓰신 책을 보세요.
볼린저 밴드 투자기법 | 존 볼린저 - 교보문고
볼린저 밴드 투자기법 | 주식을 거래하고자 하는 사람이 어떻게 볼린저 밴드를 이용하느냐에 따라 성패가 갈린다! 편견을 버리고 새로운 거래 인사이트에 눈을 뜨면 트레이딩이 달라진다 《볼
product.kyobobook.co.kr
생각보다 어렵지 않습니다.
해설본을 읽는 것보다 원조에게 듣는 설명이 좀 더.......
다음에도 재미있는 지표를 들고 오겠습니다.
'경제, 투자 > 공부하기' 카테고리의 다른 글
| [공부] RSI에 대해 다시보자 (0) | 2023.05.28 |
|---|---|
| [공부] 이동평균에 대해 다시 보자 (0) | 2023.05.25 |



댓글