[공부] 이동평균에 대해 다시 보자

구글에 가서 '이동평균'을 검색해 보면, 쩌는 결과가 나옵니다.

2700만 개

2700개도 아니고 2700만 개

이렇게나 많은 설명이 있는데 굳이 페이지를 하나 늘리는 이유는....

 

같은 내용을 얘기하더라도 조금은 다른 관점을 보여주기 위해서?

 

네 뭐 소싯적 숫자 좀 찌끄려봤다. 수학은 점수가 나쁘지 않았다.

 

그렇다면 이미 이해하는 내용일 수 있습니다.

 

 

그냥 이런 관점도 있다~ 로 봐주면 됩니다.

 

아래 이야기는 전부 차트를 설명할 때 이야기 하는 내용입니다. 정말 쉬운 내용은 건너뛰겠습니다

 

---

 

위키백과에서 '이동평균'의 의미를 찾아봅시다

와~C. 겁나 있어 보이게 설명해 놨네요.

이동평균에는 종류가 몇 가지 있지만 여기에서는 단순이동산술평균(대충 더하기만 했다는 얘기)만 얘기합니다

 

대부분의 차트에 기본적으로 들어갑니다. 

 

 

이동평균선으로 거래하는 분들도 많습니다.(전설의 BNF좌)

 

5일 이동평균이면, 5일간의 종가의 평균값입니다.

주봉의 이동평균이면, 주봉 종가의 평균값입니다.

그리고 그걸 선으로 주욱 이어서 "이동평균선(이평선)"을 만들어줍니다

 

쉽죠? 쉬운데, 아 정말 쉽나요?

 

좀 똑똑해져 봅시다. 수식을 가져올 건데 정말 쉬운 수식입니다. 겁내지 맙시다.

---

5일 이동평균 구하는 공식입니다

X는 그날의 종가를 의미합니다.

 

X를 5개 더해서 평균을 낸 값을 구했습니다.

 

그럼 다음날도 계산해 봅시다

 

 

날짜가 하나씩 늘어날 때마다 앞의 값 1개는 사라지고 뒤의 값 1개가 더해집니다.

 

간단합니다.

 

그런데 컴퓨터는 이런 식으로 계산 안 합니다. 해도 되는데, 시간이 겁나 오래 걸립니다.

5일 이평선을 보려고 차트를 100일 정도 확장해 놓으면 계산량이 나옵니다.

그런데 이평선을 하나만 보는 것도 아니죠, 몇 개씩 세팅해 놓는 경우도 있고, 이평선 외의 다른 지표들도 on.

컴퓨터가 열받겠네요.

 

 

조금 쉽게 가는 법은 없을까요?

 

식을 좀 풀어서 보겠습니다.

 

2일 차 이평식을 보죠.

 

 

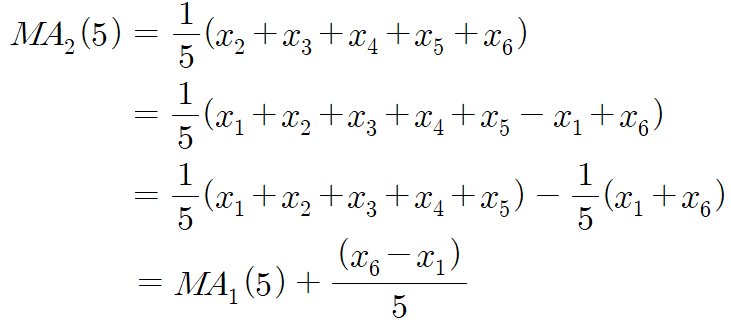
막 복잡하게 써 놨는데, 우리는 결론만 보면 됩니다.

 

 

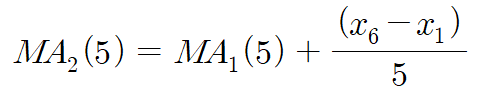
즉, 내일의 이평값을 구하기 위해서는 계산을 처음부터 할 필요 없이,

오늘의 이평값에 종가 2개를 계산해서 보정해 주면 된다.

계산량이 상당히 줄어든 게 보이죠? 우리는 지금 전기세를 아끼는 방법을 찾은 겁니다.

 

 

 

여기서 통계에 대한 개념을 한 번쯤 생각해 볼 필요가 있습니다.

평균을 계산하는 방법, 단순히 더해서 나눈다. 

 

그럼 혹시 중간에 값을 바꾸게 되면? 

 

"값을 바꿔주고 차이만큼 보정치를 더하거나 빼주면 된다"

반응형

---

 

뻔하죠? 뻔한데, 지금 이거 엄청 쉽고 단순한 예를 들어서 그렇지 정말 대단한 내용을 같이 본겁니다.

 

잠깐만 좀 똑똑해져 봅시다.

 

공학에서 "칼만필터"라는 것이 있습니다.

(제가 링크 걸어는 드릴께, 이해할라하믄 머리 아픕니다)

 

칼만 필터 - 위키백과, 우리 모두의 백과사전

 

신박한 이름은 거의 만든 사람의 이름이 따죠. 네 '루돌프 칼만'이란 분이 만들었습니다.

칼만필터의 기본 개념은 '과거와 현재의 값을 기준으로 재귀적 연산을 통해 최적의 값을 추적하는 것이다'라고 할 수 있습니다. (그니깐 대충 현재 알고있는 값으로, 모르는 값을 때려 맞춘다는 얘기)

혹시 링크 보고 왔나요?  x라 어렵습니다. 뭔 소린지 하나도 모르겠죠.

 

이게 어디에 쓰였냐면, 아폴로 우주선의 내비게이션, 로켓이나 미사일의 궤도 추적, 컴퓨터의 영상처리, 레이더 등등 뭔가 변화가 있고 상태를 측정할 수 있는 시스템에 다 쓰인다고 보면 됩니다.

 

갑자기 이게 왜 나왔냐면 우리가 봤던 위의 식들이 칼만필터중 기초에 속하는 '이동평균 필터'입니다.

네, 이걸 안다고 뭐 크게 달라지는건 없구요.

쬐끔~ 똑똑해진것에 만족하구요.

---

 

수식은 잊어도 됩니다.

그런데 그 계산 방법에 대한 개념은 머리에 탑재해 두면 좋습니다.

 

가격이 이평선을 뚫고 상승(하락)했다? 

지금의 가격이 이전 가격들과 비교해서 얼마나 올랐는지(하락했는지) 가늠이 됩니다.

 

왜 타임프레임이 큰 차트(주봉, 월봉)에서 이평선이 지지, 저항의 기준이 될 수 있는지 감이 옵니다.

 

 

 

이런 해석이 새로운 것은 아니지만 약간이라도 이해의 장을 넓혔으면 합니다.